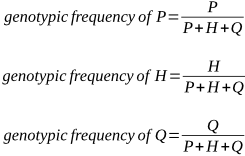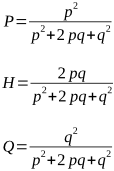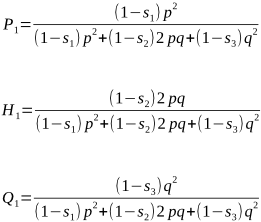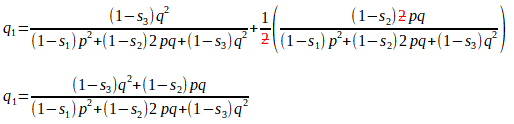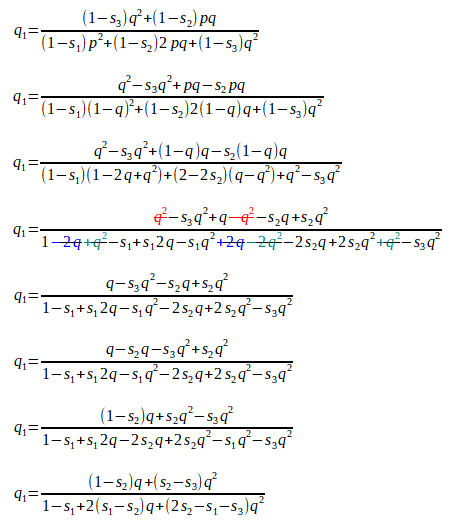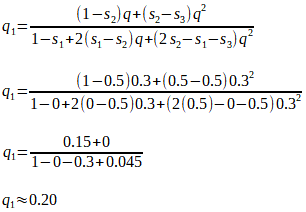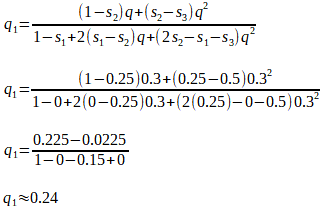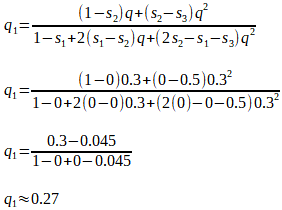The Better Breeding Blog Breed Better Animals

This post revisits several concepts discussed in the Population Genetics category. I’ve linked to the relevant pages as they come up below if you need a refresher.

Assume a locus A with alleles A₁ and A₂. Either could be, but is not necessarily, dominant or recessive to the other.

p is the gene frequency of the A₁ allele and q is the gene frequency of the A₂ allele. (Similarly, p and q as used here do not necessarily ascribe dominance or recessiveness to either allele.)

P is the genotypic frequency of the A₁A₁ genotype.
H is the genotypic frequency of the A₁A₂ genotype.
Q is the genotypic frequency of the A₂A₂ genotype.

Remember that P + H + Q = 1. If there are three genotypes in a population, the proportion of each as a percentage (its frequency) must add up to 100%, or 1.

We can express the proportions of P, H and Q as:

Assume these frequencies occur in a population from which parents have not yet been selected to produce the next generation.
If their parents were randomly mated, then this population should be in a Hardy-Weinberg equilibrium, thus:

P = p²
H = 2pq
Q = q²

Substituting these values into the formulae above, we get:

But we need to take into account the degree of dominance with respect to fitness for each of the genotypes A₁A₁, A₁A₂ and A₂A₂.
Let s₁ be the relative fitness difference for A₁A₁.
Let s₂ be the relative fitness difference for A₁A₂.
Let s₃ be the relative fitness difference for A₂A₂.

If A₁A₁ is the fittest genotype (produces the most offspring), then its fitness difference, relative to itself, is s₁ = 0, and its relative fitness is (1 - s₁) = (1 - 0) = 1.

If, hypothetically, the A₁A₂ genotype produces 25% fewer offspring than the A₁A₁ genotype, then the fitness difference, relative to the fittest genotype A₁A₁, is s₂ = 0.25, and the relative fitness is (1 - s₂) = (1 - 0.25) = 0.75. We can say that the A₁A₂ genotype is 75%, or 0.75 as fit as the A₁A₁ genotype.

More generally, we can say that:
the relative fitness value for A₁A₁ is (1 - s₁),
the relative fitness value for A₁A₂ is (1 - s₂), and
the relative fitness value for A₂A₂ is (1 - s₃).

In other words:
the relative fitness of A₁A₁ is (1 - s₁) of its genotypic frequency P, or
(1 - s₁) × P = (1 - s₁) × p² = (1 - s₁) p²

Similarly, we can state the relative fitness of A₁A₂ as (1 - s₂)2pq, and the relative fitness of A₂A₂ as (1 - s₃)q².

We wish to select animals from this population to be the parents of the next generation. From this, their progeny become the next parents, with genotypic frequencies of P₁, H₁ and Q₁. Can you see how the following formulae are the same as above, but this time we have taken into consideration the relative fitness values for each of P₁, H₁ and Q₁:

In The Effect of Mating Systems on Gene and Genotypic Frequencies: Outbreeding, we saw how the gene frequency q = Q + ½H.

From this, the frequency of the A₂ allele after selection is:

Substituting for Q₁ and H₁, we get:

[Here we have ’simply’ added two (elaborate) fractions with a common denominator. This is just ^a/_c + ^b/_c = ^a + b/_c on steroids!]

As there are just two alleles A₁ and A₂, with the respective gene frequencies p  and q , these must add up to one, as p + q = 1. We can rewrite this as p = 1 - q.
We can substitute (1 - q)  for p, cancel some terms, and rearrange the rest to get:

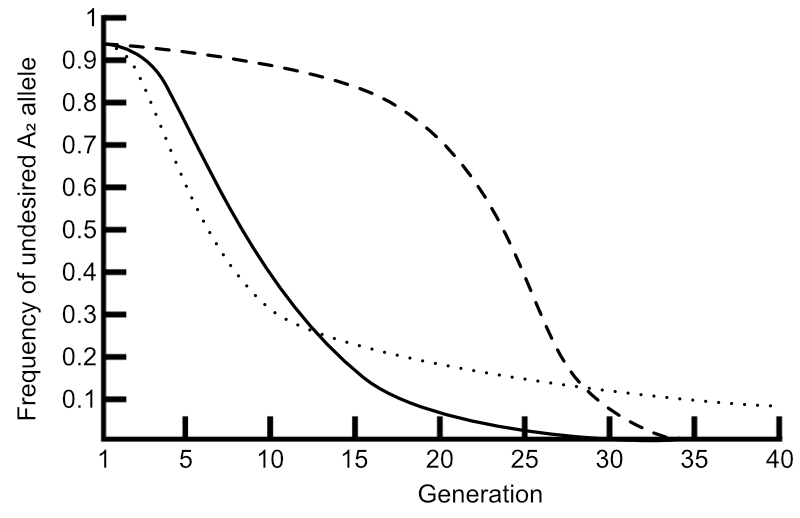
We now have a formula with which we can calculate the new gene frequency in the next population, given the initial gene frequency, the degree of dominance (if any), and the difference in fitness values (if any) of the various genotypes.

Next week we’ll run through some scenarios to see this in practice!

Last week we derived a formula for calculating change in gene frequencies, given the initial gene frequency, the degree of dominance (if any), and the difference in fitness values (if any) of the various genotypes.

This week we’ll use that formula as it could apply in real-life.

Let’s revisit the following graph from Effectiveness of Selection: Initial Gene Frequency and Fitness Differences:

Assume that the ‘A₂‘ allele is undesired at the ‘A’ locus, and has a gene frequency q of 0.3. Assume too that the ‘A₂‘ allele is completely dominant, and with respect to fitness, that the A₁A₂ and A₂A₂ genotypes produce half as many offspring relative to the A₁A₁ genotype. Thus:

s₁ = 0
s₂ = 0.5
s₃ = 0.5

and

Let’s now assume that there is no dominance at the ‘A’ locus. With respect to fitness, the A₁A₂ genotype produces 25% fewer offspring relative to the A₁A₁ genotype, while the A₂A₂ genotype produces half as many offspring relative to the A₁A₁ genotype.

s₁ = 0
s₂ = 0.25
s₃ = 0.5

and

But what if ‘A₂‘ was completely recessive? Assume that the A₁A₂ genotype produces as many offspring relative to the A₁A₁ genotype, while the A₂A₂ genotype produces half as many offspring relative to the A₁A₁ genotype.

s₁ = 0
s₂ = 0
s₃ = 0.5

and

We have shown how, in one generation of selection, that the frequency q of the ‘A₂‘ allele drops noticeably from 0.3 to 0.2 if completely dominant. This is less marked if there is no dominance at the ‘A’ locus, where the frequency drops slightly from 0.3 to 0.24. The change in frequency is even less if the allele is completely recessive, from 0.3 to 0.27. These values can be seen graphically — below is the same graph as above, but with the inital gene frequency q = 0.3 marked with a red line. You can see how the steepness (change in frequency) differs for each line between where each begins at q = 0.3 (read this as generation 0) and one generation later (further to the right along the x-axis).

This concludes the Selection Strategies: Simply Inherited Traits section.