Explaining the Maths
This post explains the maths behind the formula 3n × 2m (the number of unique zygotes) mentioned in last week’s post.
Let’s go back to that three-locus Punnett square, where both parents are heterozygous at A, B and C. We determined visually — and not that easily! — that there are 27 unique genotypes (colour-coded here):

© Optimate Group Pty Ltd
Break each of the three loci into three individual squares:
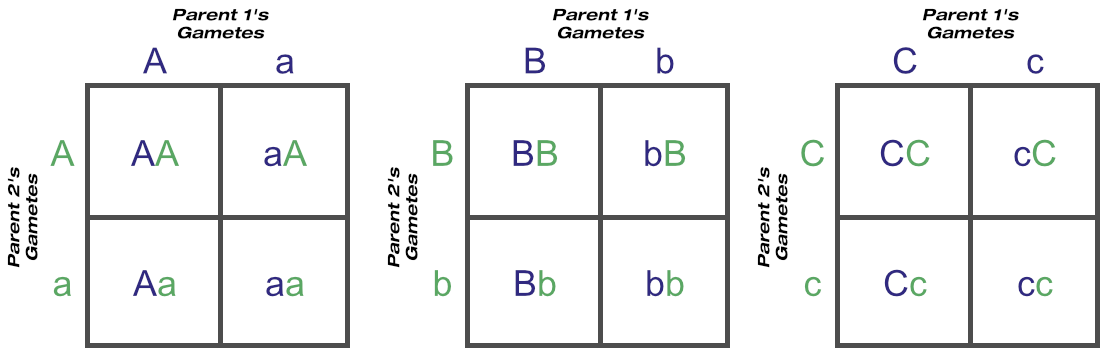
© Optimate Group Pty Ltd
While there are four possible arrangements, there are three unique genotypes from each locus (remember that Aa and aA, Bb and bB, and Cc and cC are the same), so long as both parents are heterozygous at each.
Thus every possible zygote from those two parents would have a genotype comprised of (AA or Aa or aa) and (BB or Bb or bb) and (CC or Cc or cc).
In statistics, where we’d say ‘or’, we’d write ‘+’, and where we’d say ‘and’, we’d write ‘×’.
Thus there are (any three of A) × (any three of B) × (any three of C) =3 × 3 × 3 = 33 = 27 unique genotypes possible.
Similarly you could go back to a simpler two-locus Punnett square, where we already know there are nine unique genotypes:
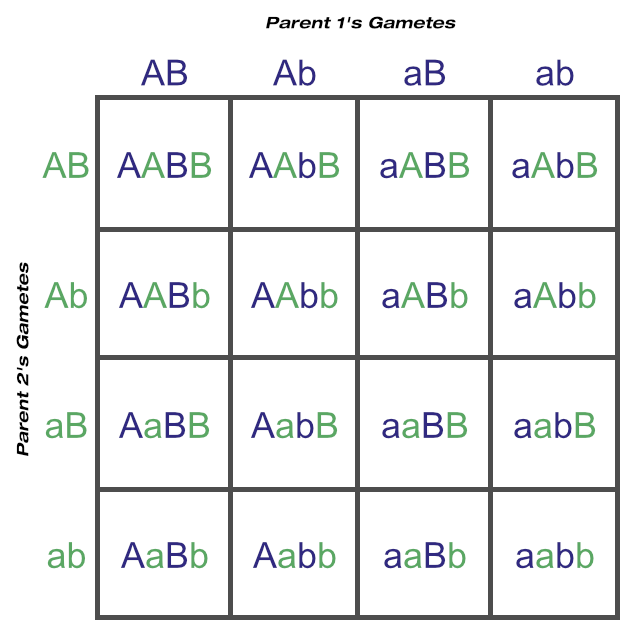
© Optimate Group Pty Ltd
and confirm that there are (any three of AA or Aa or aa) × (any three of BB or Bb or bb) =3 × 3 = 32 = 9 unique genotypes possible.
And without even attempting to draw a four-locus Punnett square (!!), we could calculate the number of unique genotypes for two parents heterozygous at four loci to be (any three of A) × (any three of B) × (any three of C) × (any three of D) =3 × 3 × 3 × 3 = 34 = 81 unique genotypes possible.
Hopefully it’s much clearer now where the 3 in 3n comes from, and why it’s to the power of n loci? (Always remember that this is when both parents are heterozygous at n loci.)
But what about the 2m component of the formula, where m is the number of additional loci only one parent is heterozygous at?
Let’s go back to a two-locus Punnett square, but this time with only one heterozygous parent at one locus:
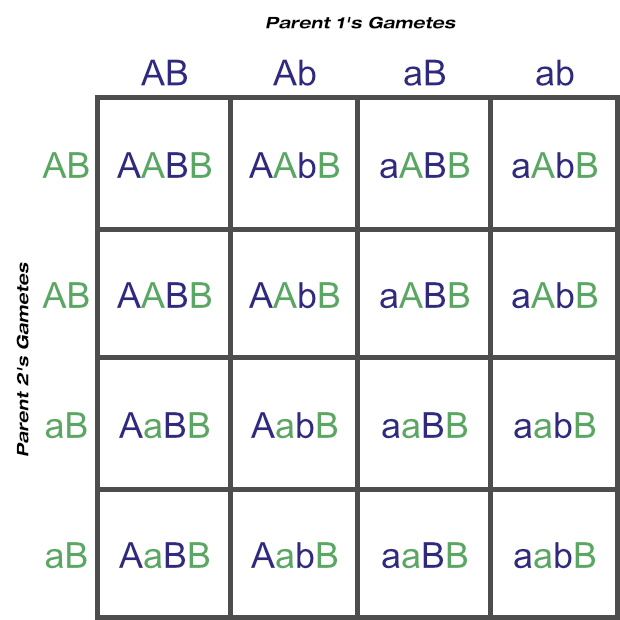
© Optimate Group Pty Ltd
You can see that there are, in a sense, two duplicate sets, as parent 2 can only ever contribute a ‘B’ allele. It has no ‘b’, and because of this the number of unique genotypes at this locus is determined solely by parent 1. As there is no second ‘b’ to join up with another ‘b’, the three genotypes AAbb, Aabb and aabb can’t be formed.
The number of unique genotypes thus drops from nine:
AABB AABb AaBB AaBb AAbb Aabb aaBB aaBb aabb
to six:
AABB AABb AaBB AaBb aaBB aaBb
The possible genotypes at the A locus are still (AA or Aa or aa) but the possible genotypes at the B locus are limited to (BB or Bb). ‘bb’ is never possible.
Thus every possible zygote is now (AA or Aa or aa) and (BB or Bb).
Or, (any three of A) × (any two of B) =3 × 2 = 6 unique genotypes possible.
Let’s add another locus, C, for which parent 2 this time is heterozygous. As with B, the possible genotypes are CC or Cc.
Every possible zygote is now (any three of A) × (any two of B contributed by parent 1) × (any two of C contributed by parent 2) =3 × 2 × 2 = 3 × 22 = 12 unique genotypes possible.
Can you see how it doesn’t matter which parent is heterozygous at which locus? Parent 1 could have been heterozygous at both loci B and C, or parent 2, and the end result would be the same.
Let’s now work through all possible unique genotypes when two parents are heterozygous at two loci (A and B), and one parent is heterozygous at two additional loci (C and D), by combining what we’ve covered above:
The number of possible genotypes is (AA or Aa or aa) and (BB or Bb or bb) and (CC or Cc) and (DD or Dd).
Or, (any three of A) × (any three of B) × (any two of C) × (any two of D) =3 × 3 × 2 × 2 = 32 × 22 = 36 unique genotypes possible.
What about a fifth locus, E, at which both parents are heterozygous, and a sixth one, F, at which just one is heterozygous?
(any three of A) × (any three of B) × (any three of E) × (any two of C) × (any two of D) × (any two of F) =3 × 3 × 3 × 2 × 2 × 2 = 72 unique genotypes possible.
Or, 33 × 23.
The more variations of these combinations of heterozygous loci you construct, the more clear it is to see the pattern, or the formula 3n × 2m, where n is the number of heterozygous loci both parents have, and m is the number of heterozygous loci one parent has.
Please do note that this assumes only two alleles exist for each locus. As mentioned last week, many genes do contain three, four, or even more alleles, which does complicate the maths, but the important thing here is that you can see how 3n × 2m was derived in the first place, and hopefully I’ve done that here for you.
Leave a comment